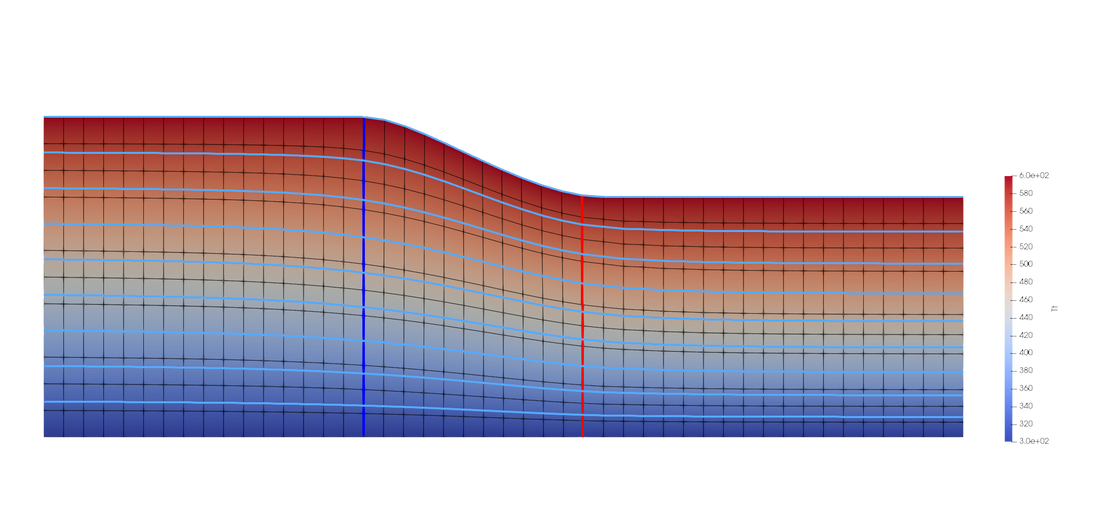
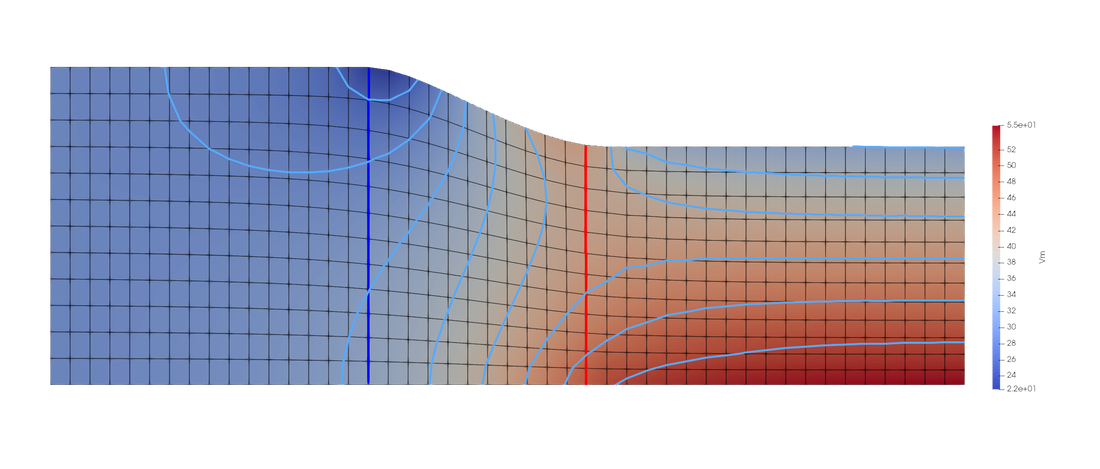
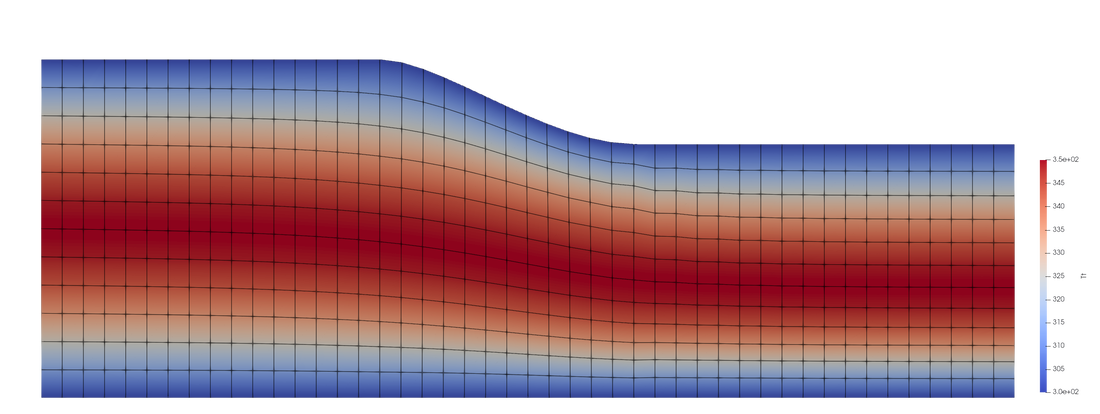
Empty channel vs standard CFD code
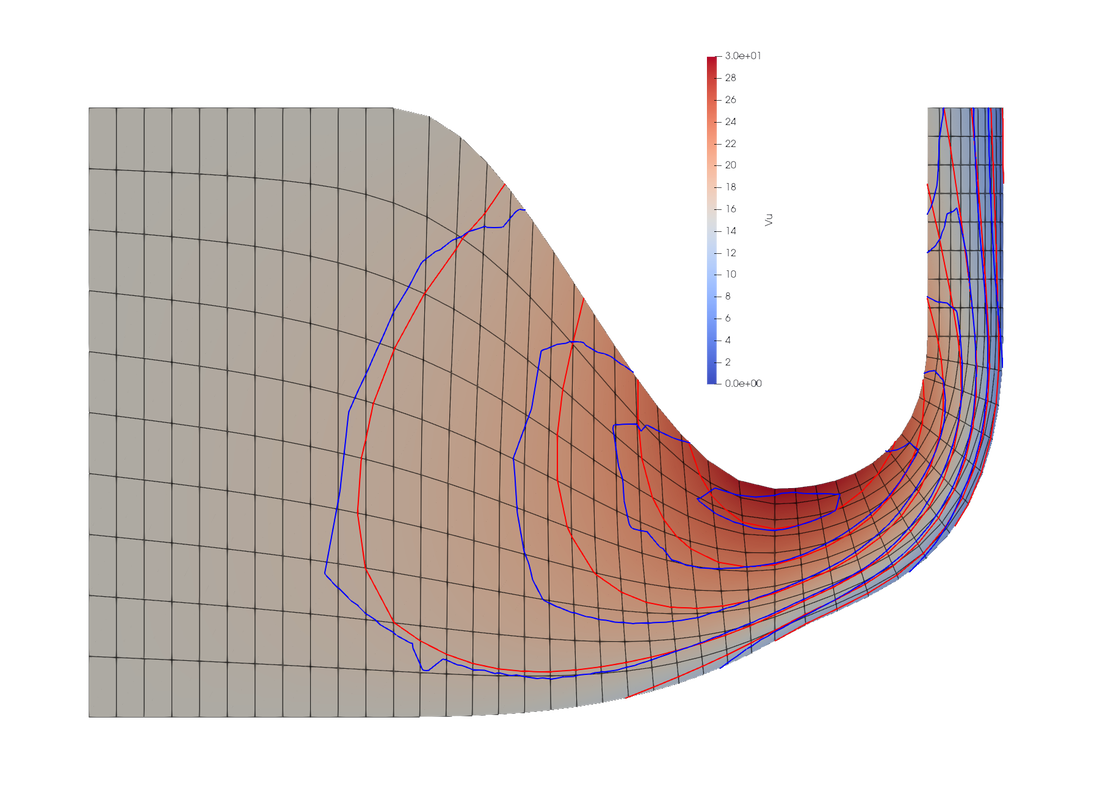
Comparisons with 3D CFD code results, configuration is inviscid and incompressible, the reference is in red. For a fair comparison, Yams also uses constant density .
After the turn 3D CFD code shows a recirculation, witch of course can not be simulated by a curvature solver but it's interesting to not that it does not affect the excellent matching of results. On this mesh computation takes 200ms to reach 0.01% of residual on stream lines positions.
This test case validates:
After the turn 3D CFD code shows a recirculation, witch of course can not be simulated by a curvature solver but it's interesting to not that it does not affect the excellent matching of results. On this mesh computation takes 200ms to reach 0.01% of residual on stream lines positions.
This test case validates:
- Derivatives on irregular grid.
- Influence of the curvature.
- Streamlines relocation.
Tangential velocity comparison
|
Meridional velocity comparison
|
Flow with constant angle, analytical solution
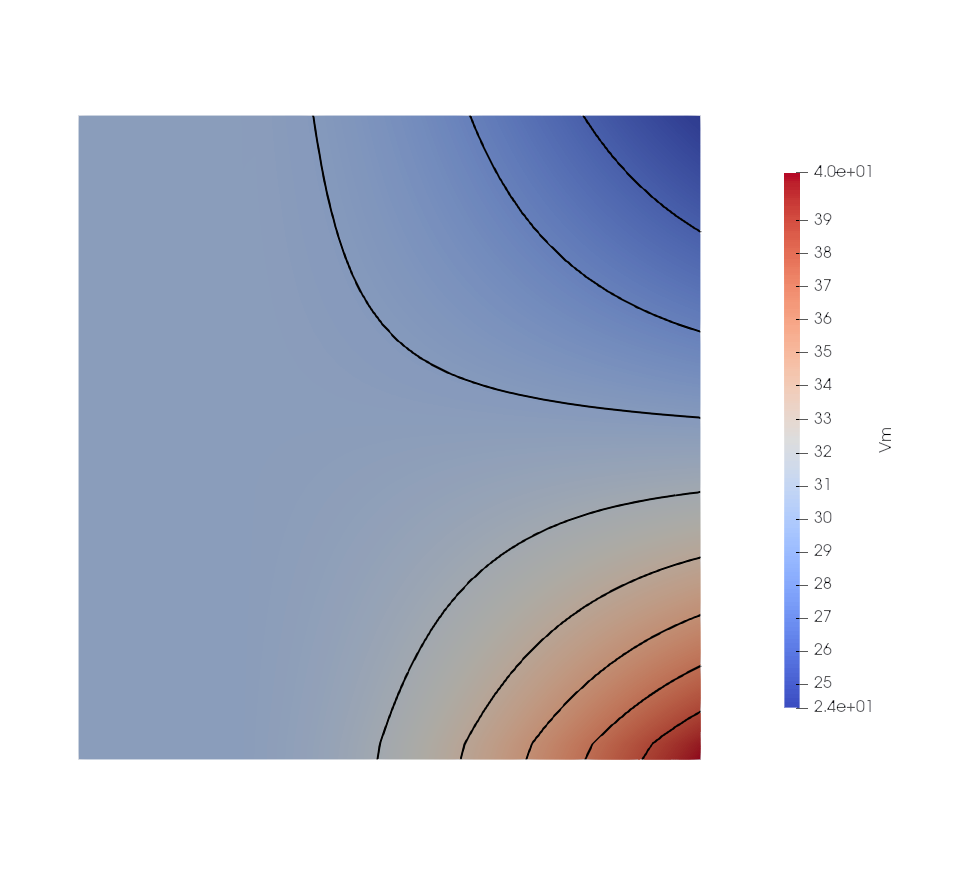
Comparison of the influence of the turning angle with the constant flow angle, without curvature, isentropic and isoenergetic analytical case. This test validate the tangential term of the equation.
|
Under these conditions the radial equilibrium equation resumes to:
\[V_{m}\frac{dV_{m}}{dm}=-V_{u}\frac{V_{u}}{r}\frac{d\left(rV_{u}\right)}{dr}\] Since
\[V_{u}=V_{m}\tan\left(\alpha\right)\] Then
\[\frac{V_{m}}{V_{mi}}=\left(\frac{r_{i}}{r}\right)^{\sin^{2}\alpha}\] The analytical solution is:
\[\frac{dV_{m}}{dm}=-\sin^{2}\alpha\frac{dr}{r}\] |
|
With a fine grid and under span constant imposed deviation up to 60 degrees, computation made with Yams solver shows an agreement with a maximum error below 1%.
Continuity at equation switch.
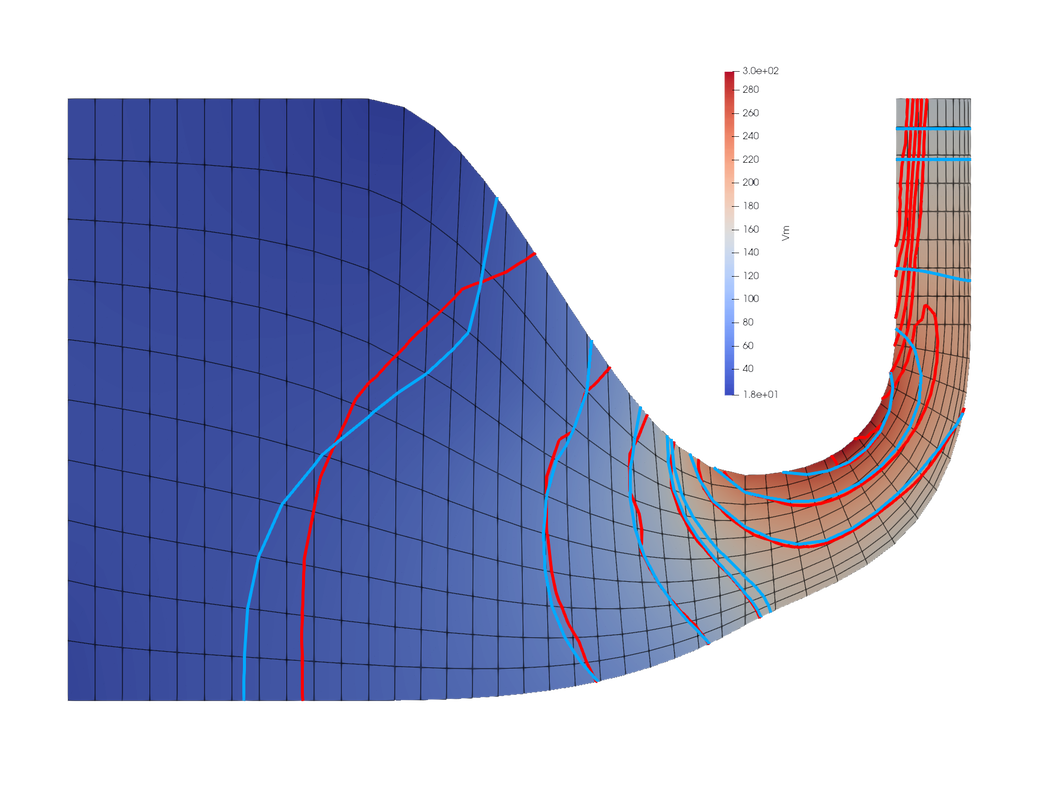
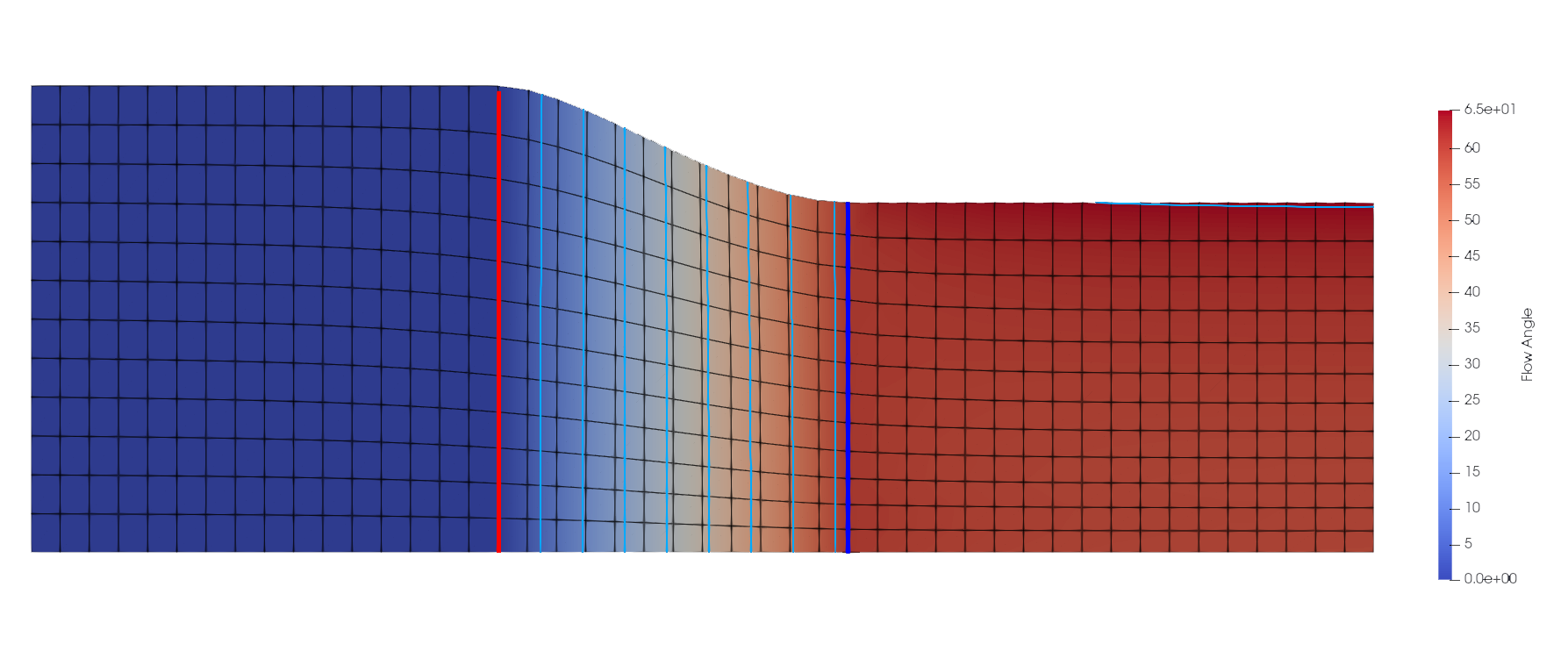
The solver is using 2 sets of equations, one for design and channel with no blade, the other for analysis, on this test case we validate the continuity thru leading/trailing edges of the velocities. This test represent a convergent nozzle with a deviation of 65° with an hentalpy span gradient.
As the flow is isoenergetic total temperature contours follows stream lines.
The meridional velocity shows no discontinuity at blade's interfaces where equation set switch occurs.
The equations set takes into account entropy and enthalpy span gradients and enthalpy stream gradient.
\[ \frac{\partial S}{\partial q}, \frac{\partial H}{\partial q}, \frac{\partial S}{\partial m} \]
For the following test case we add an enthalpy span profile.
In spite of the perturbation, the meridional velocity manage to converge,
